By Nishithe Welandawe
The following is a breakdown of a problem I worked on while I was Interning at WealthOS over the summer. A bit about WealthOS, it is an API first, enterprise, core wealth management platform built to accelerate digital adoption and innovation within the wealth management industry.
Framing the Problem
Let's say you (the reader) and I both have our pensions managed by a fictitious company easyPensions. One fine business day I feel like buying five shares of $AAPL because I feel like the stock will go up. You wake up to the same news and wish to buy 50 shares of the same. Now a trader/computer at easyPensions has two options;
- Send two separate orders of 50 & 5 to the market.
- Send an order of 55 shares to the market
The latter turns out to be what we want because of the simple constraint of transaction costs. By grouping orders together we can reduce the overall transaction costs per order. The reasons why this is possible dives in too deep into how accounts are held at easyPensions to get into right now.
Now easyPensions wants to let their clients trade not only equities but also things like Funds. Let's complicate the problem a bit further,
- I can now ask for $100 of $APPL instead of x shares.
- The price of the stock is dynamic and changes between sending the order and execution.
- Computers don't store rational numbers well
For the sake of example, assume Anton wants to buy a $100 of $AAPL. You and I want to get in on the action and place the exact same order. easyPensions goes to a Market Maker/ Broker and asks for $300 worth of shares in Apple for which he receives 10 shares. Now how does easyPensions give Anton, you, and myself what we asked for? Assume that the computers only store up to 2 decimals for shares.

Now we come to the question of what happens to that 0.01. Across a single transaction, it might not seem like much but across hundreds and thousands of daily transactions like this, it adds up.
Therefore one has to decide what to do with the error terms that keep adding up. Possible solutions include,
- Assigning them to one big “house accounts”; an account where decimals go to die.
- Random Assignment
- Socialism; assignment to the smallest order in the lot
One could argue the merits of each of the solutions but ultimately we decided to provide support for the house account and “Socialism”.
As with any decision when it comes to business logic, untested logic could seem fine on day 1 of production through to day 100 and implode on the 101st day. So before we moved on to production, I started framing the problem quantitatively and wanted to test its limitations and implications.
Simulating the Business Logic
There are two ways to test the algorithm,
- Test it on the live platform ( dangerous, haphazard)
- Run a simulation
The latter is the obvious choice. Since this process is not a common process it required me to build a structure to emulate a market, trading accounts and trades. Below is a little snippet to create an investor class.

Much like a real investor who would have capital and assets.
The next would be to create a concept of a market. Which would require assets and their prices. For the market I used real-world time series for 2 funds; each at different unit price points.
From there we created a class and function to do the actual trading. We assume that amongst a fixed pool of investors for each day each accounts buys random number of units. The random number is sampled from a Poisson distribution with parameter equal to the mean order quantity/value. This form of repeated sampling from a distribution is what tells us how our process performs under random conditions. Running this sampling many 1000s of times hopefully will bring us closer to how the algorithm will actually perform.
Then orders are aggregated and the remainder is calculated and assigned to the smallest investor.
Based on this I asked the following questions,
- How does the remainder change based on the Closing price?
- How does the mean order value affect it?
- What is the relationship between the size of the order pool and the remainder?
By varying parameters and visualising the data, we began to understand what is properties are invariant to parameters and final risk.

From there we can gather even more data and using statistical tests gain inferences.
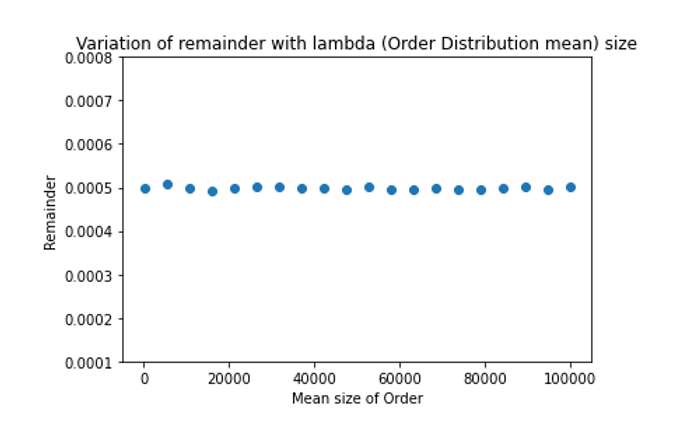
As an example, the above plot shows how the remainder is stable with respect to the mean order size. In plain English; even if people place larger orders that will not affect how we aggregate orders.
I hope you enjoyed a taste of simple methods used at WealthOS to verify that the backend logic isn't going to blow up one day when the Market opens. I hope that you'll be using simple simulations like this for your next idea or project too!
Follow Nishithe on Medium if you want to keep up to date on his work.
